Kuželosečky

Kuželosečka je rovinná křivka, která vznikne jako průnik roviny s rotační kuželovou plochou, přičemž rovina neprochází jejím vrcholem (citace Wikipedie).

Apolloniova definice kuželoseček.

Asi není nastaveno vykreslování obrázků!

Seznámíme se se základními vlastnostmi elipsy, paraboly a hyperboly, pro které (spolu s kružnicí) užíváme společný název kuželosečky. Každou z nich je možné sestrojit jako průsečnou křivku rotační kuželové plochy rovinou.

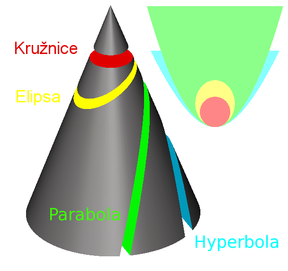
Pokud rovina řezu neprochází vrcholem, je řezem tzv. jednoduchá (vlastní, regulární) kuželosečka.

Řezy rovinou procházející vrcholem označujeme jako složené (degenerované, nevlastní, singulární) kuželosečky (dvě přímky různoběžné, dvě přímky totožné, jeden bod). Ke složeným kuželosečkám patří i dvě přímky rovnoběžné.

Zdůrazněme ještě, že kuželosečky jsou křivky rovinné (jsou to řezy rovinou).

Elipsa

je tvořena všemi body M roviny, které mají od dvou různých pevných bodů F₁ , F₂ této roviny (ohnisek) stálý (konstantní) součet vzdáleností 2a , přičemž platí: 2a > |F₁F₂|

Pro body M elipsy platí: |F₁M| + |F₂M| = 2a

(zahradnická) konstrukce elipsy
proužková konstrukce elipsy (součtová, rozdílová)
Vezmeme proužek papíru na který naneseme velikosti obou poloos elipsy. Vyznačené body X , Y přiložíme na osy elispy a pokud papírem pohybujeme, pak bod M opisuje elipsu.
(hyper)oskulační kružnice elipsy
Oskulační kružnice (Wikipedie) rovinné křivky v určitém bodě je kružnice, která tímto bodem prochází, má zde s danou rovinnou křivkou společnou první derivaci (společnou tečnu v tomto bodě) a rovněž i druhou derivaci (co nejvíce se v okolí tohoto bodu křivce přimyká).
V okolí vrcholu (ať již hlavního, či vedlejšího) ji často nazýváme hyperoskulační kružnicí.
Rytzova konstrukce elipsy
Každá přímka procházející středem elipsy je jejím průměrem. Tečny sestrojené v koncových bodech jednoho sdruženého průměru jsou rovnoběžné s druhým sdruženým průměrem. Zmíněnou konstrukcí získáme osy elipsy.
tečny elipsy z vnějšího bodu (rozbor, konstrukce) a rovnoběžné se směrem.
elipsa jako afinní obraz kružnice

Kružnice:

je skupina (souhrn) všech bodů M v rovině, které leží ve stejné vzdálenosti, označované jako poloměr r , od pevně daného bodu S , zvaného střed.

Pro body M kružnice platí : |SM| = r

Kružnice je tedy speciálním případem elipsy, u které obě ohniska a střed splynou v jediný bod.

Parabola:

je množina všech bodů M roviny, které mají od pevného bodu F (ohnisko) a od pevné přímky d (řídící přímka), která tímto bodem neprochází, stejnou vzdálenost.

Pro body M paraboly platí: |FM| = |dM|

definice
subtangenta a subnormála
konstrukce paraboly,
vlastnosti paraboly,
(hyper)oskulační kružnice paraboly,
tečny paraboly z vnějšího bodu a rovnoběžné se směrem.

Hyperbola:

je množina všech bodů M roviny o daném (stálém, konstantním) rozdílu vzdáleností od dvou různých pevně daných bodů – ohnisek. Tento rozdíl je menší, než je vzdálenost obou ohnisek.

Pro body M hyperboly platí: |F₁M| - |F₂M| = 2a

definice hyperboly,
kostrukce hyperboly
(hyper)oskulační kružnice hyperboly,
tečny hyperboly

Zpět na harmonogram cvičení